拡散確率モデル : (2) イントロダクション (翻訳/解説)

翻訳 : (株)クラスキャットセールスインフォメーション
作成日時 : 09/20/2022 (No releases published)

* 本ページは、Denoising diffusion probabilistic models の以下のドキュメントを翻訳した上で適宜、補足説明したものです：

README.md
Diffusion probabilistic models – Introduction (Author : Philippe Esling (esling@ircam.fr))

* サンプルコードの動作確認はしておりますが、必要な場合には適宜、追加改変しています。
* ご自由にリンクを張って頂いてかまいませんが、sales-info@classcat.com までご一報いただけると嬉しいです。

クラスキャット人工知能研究開発支援サービス

◆ クラスキャットは人工知能・テレワークに関する各種サービスを提供しています。お気軽にご相談ください :

人工知能研究開発支援
1. 人工知能研修サービス(経営者層向けオンサイト研修)
2. テクニカルコンサルティングサービス
3. 実証実験(プロトタイプ構築)
4. アプリケーションへの実装
人工知能研修サービス
PoC(概念実証)を失敗させないための支援

◆ 人工知能とビジネスをテーマに WEB セミナーを定期的に開催しています。スケジュール。

お住まいの地域に関係なく Web ブラウザからご参加頂けます。事前登録 が必要ですのでご注意ください。

◆ お問合せ : 本件に関するお問い合わせ先は下記までお願いいたします。

株式会社クラスキャット セールス・マーケティング本部セールス・インフォメーション
sales-info@classcat.com ; Web: www.classcat.com ; ClassCatJP

拡散確率モデル (2) イントロダクション

この 2 番目のノートブックは私たちの 4 つのノートブックシリーズで拡散確率モデル [1] の探求を続けます。

スコアマッチングとランジュバン動力学。
拡散確率モデルとノイズ除去
WaveGrad による waveforms への応用。
推論を高速化するための暗黙モデル

ここで、前のノートブックで見たスコアマッチング [3] とランジュバン動力学の基本を素早くおさらいします。それから、熱力学に基づく拡散確率モデルのオリジナルの定式化 [2]、そしてより最近のノイズ除去の定式化 [1] を紹介します。

理論的基盤 – 素早い要約

このセクションでは前のノートブックからのスコアマッチングの素早い要約を提供します、依然としてスイスロール・データセットに基づいています。

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_swiss_roll
from helper_plot import hdr_plot_style
hdr_plot_style()
# Sample a batch from the swiss roll
def sample_batch(size, noise=0.5):
    x, _= make_swiss_roll(size, noise=noise)
    return x[:, [0, 2]] / 10.0
# Plot it
data = sample_batch(10**4).T
plt.figure(figsize=(16, 12))
plt.scatter(*data, alpha=0.5, color='red', edgecolor='white', s=40);

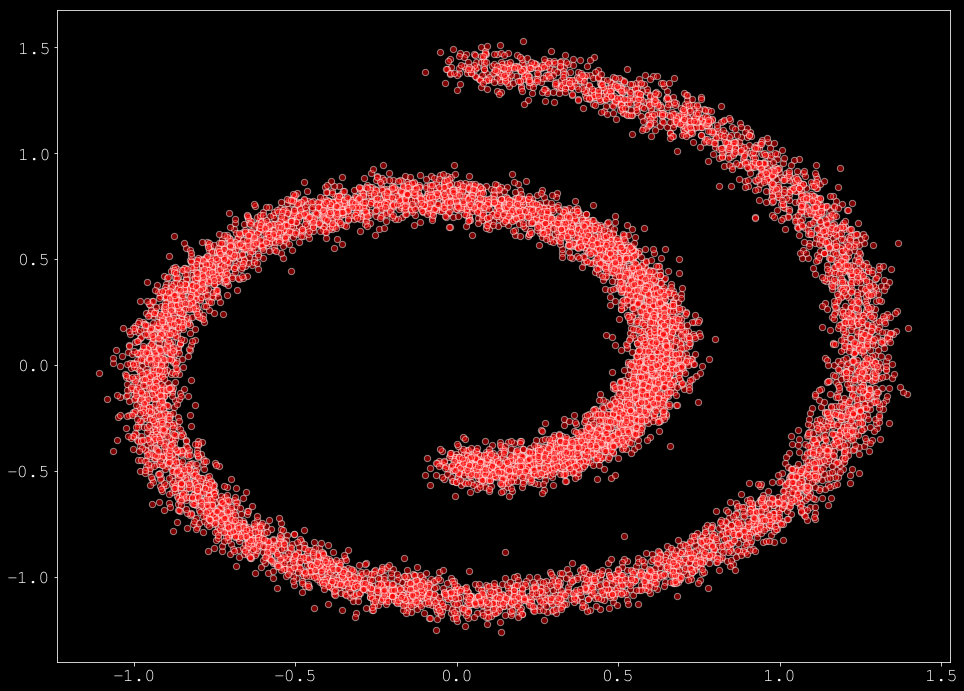
スコアマッチング

スコアマッチングは、$\log p(\mathbf{x})$ を直接学習する代わりに、$x$ に関する $\log p(\mathbf{x})$ の勾配 (スコアと呼称) を学習することを目標とします。従って、次を近似するモデルを探求します :

\[
\mathcal{F}_{\theta}(\mathbf{x}) \approx \nabla_{\mathbf{x}} \log p(\mathbf{x})
\]

このモデルを MSE objective で最適化することは次を最適化することと等価であることを見ました :

\[
\mathcal{L}_{matching} = E_{\mathbf{x} \sim p(\mathbf{x})} \left[ \text{ tr}\left( \nabla_{\mathbf{x}} \mathcal{F}_{\theta}(\mathbf{x}) \right) + \frac{1}{2} \left\Vert \mathcal{F}_{\theta}(\mathbf{x}) \right\lVert_2^2 \right]
,
\]

ここで $\nabla_{\mathbf{x}} \mathcal{F}_{\theta}(\mathbf{x})$ は $x$ に関する $\mathcal{F}_{\theta}(\mathbf{x})$ のヤコビアンを示します。この定式化に伴う問題はこのヤコビアンの計算にあります、これは高次元データに上手くスケールしません。これは scliced スコアマッチングのより効率的な定式化に繋がり、これは以下によりヤコビアンの計算を近似するためにランダム射影に頼ります :

\[
E_{\mathbf{v} \sim \mathcal{N}(0, 1)} E_{\mathbf{x} \sim p(\mathbf{x})} \left[ \mathbf{v}^T \nabla_{\mathbf{x}} \mathcal{F}_{\theta}(\mathbf{x}) \mathbf{v} + \frac{1}{2} \left\Vert \mathbf{v}^T \mathcal{F}_{\theta}(\mathbf{x}) \right\lVert_2^2 \right]
,
\]

ここで $\mathbf{v} \sim \mathcal{N}(0, 1)$ は正規分布のベクトルのセットです。これは計算的に効率的で、以下の実装で示されるように、foward モードの自動微分を使用して計算できることが示されています :

import torch
import torch.nn as nn
import torch.optim as optim
def sliced_score_matching(model, samples):
    samples.requires_grad_(True)
    # Construct random vectors
    vectors = torch.randn_like(samples)
    vectors = vectors / torch.norm(vectors, dim=-1, keepdim=True)
    # Compute the optimized vector-product jacobian
    logp, jvp = autograd.functional.jvp(model, samples, vectors, create_graph=True)
    # Compute the norm loss
    norm_loss = (logp * vectors) ** 2 / 2.
    # Compute the Jacobian loss
    v_jvp = jvp * vectors
    jacob_loss = v_jvp
    loss = jacob_loss + norm_loss
    return loss.mean(-1).mean(-1)

ノイズ除去スコアマッチング

元々は、ノイズ除去スコアマッチングは Vincent [3] によりノイズ除去オートエンコーダのコンテキストで考察されました。私たちのケースでは、分布 $q_{\sigma}(\tilde{\mathbf{x}}\mid\mathbf{x})$ により入力を corrupt させて、スコアマッチングの計算で $\nabla_{\mathbf{x}} \mathcal{F}_{\theta}(\mathbf{x})$ (訳注: $x$ に関する $\mathcal{F}_{\theta}(\mathbf{x})$ のヤコビアン) の使用を完全に取り除くことができます。最適なネットワーク $\mathcal{F}_{\theta}(\mathbf{x}) \approx \nabla_{\mathbf{x}} \log p(\mathbf{x})$ は次の目的関数を最小化することで見つけられることが分かっています :

\[
E_{q_{\sigma}(\tilde{\mathbf{x}}\mid\mathbf{x})} E_{\mathbf{x} \sim p(\mathbf{x})} \left[ \left\Vert \mathcal{F}_{\theta}(\tilde{\mathbf{x}}) – \nabla_{\tilde{\mathbf{x}}} \log q_{\sigma}(\tilde{\mathbf{x}}\mid\mathbf{x}) \right\lVert_2^2 \right]
,
\]

重要な点は、$\mathcal{F}_{\theta}(\mathbf{x}) = \nabla_{\mathbf{x}} \log q_{\sigma}(\mathbf{x}) \approx \nabla_{\mathbf{x}} \log p(\mathbf{x})$ はノイズが十分に小さく$q_{\sigma}(\mathbf{x}) \approx p(\mathbf{x})$ であるときに限り真であることです。[3], [8] で示されたように、ノイズ分布を $q_{\sigma}(\tilde{\mathbf{x}}\mid\mathbf{x})=\mathcal{N}(\tilde{\mathbf{x}}\mid\mathbf{x}, \sigma^{2}\mathbf{I})$ であるように選択した場合、$\nabla_{\tilde{\mathbf{x}}} \log q_{\sigma}(\tilde{\mathbf{x}}\mid\mathbf{x}) = \frac{\tilde{\mathbf{x}} – \mathbf{x}}{\sigma^{2}}$ を得ます。従って、ノイズ除去スコアマッチング損失は単純に以下になります :

\[
\mathcal{l}(\theta;\sigma) = E_{q_{\sigma}(\tilde{\mathbf{x}}\mid\mathbf{x})} E_{\mathbf{x} \sim p(\mathbf{x})} \left[ \left\Vert \mathcal{F}_{\theta}(\tilde{\mathbf{x}}) + \frac{\tilde{\mathbf{x}} – \mathbf{x}}{\sigma^{2}} \right\lVert_2^2 \right]
,
\]

ノイズ除去スコアマッチング損失を以下のように実装できます :

def denoising_score_matching(scorenet, samples, sigma=0.01):
    perturbed_samples = samples + torch.randn_like(samples) * sigma
    target = - 1 / (sigma ** 2) * (perturbed_samples - samples)
    scores = scorenet(perturbed_samples)
    target = target.view(target.shape[0], -1)
    scores = scores.view(scores.shape[0], -1)
    loss = 1 / 2. * ((scores - target) ** 2).sum(dim=-1).mean(dim=0)
    return loss

最適化については、$\mathcal{F}_{\theta}(\mathbf{x})$ を任意のタイプのニューラルネットワークとして定義することにより、このプロセスの非常に単純な実装を遂行できます。以下のように最小限必要な実装を行なうことができます :

# Our approximation model
model = nn.Sequential(
    nn.Linear(2, 128), nn.Softplus(),
    nn.Linear(128, 128), nn.Softplus(),
    nn.Linear(128, 2)
)
# Create ADAM optimizer over our model
optimizer = optim.Adam(model.parameters(), lr=1e-3)
dataset = torch.tensor(data.T).float()
for t in range(5000):
    # Compute the loss.
    loss = denoising_score_matching(model, dataset)
    # Before the backward pass, zero all of the network gradients
    optimizer.zero_grad()
    # Backward pass: compute gradient of the loss with respect to parameters
    loss.backward()
    # Calling the step function to update the parameters
    optimizer.step()
    # Print loss
    if ((t % 1000) == 0):
        print(loss)

tensor(9996.8447, grad_fn=<MulBackward0>)
tensor(10036.8750, grad_fn=<MulBackward0>)
tensor(10104.2119, grad_fn=<MulBackward0>)
tensor(9976.1631, grad_fn=<MulBackward0>)
tensor(9974.6611, grad_fn=<MulBackward0>)

入力空間に渡り出力値をプロットすることで $\mathcal{F}_{\theta}(\mathbf{x}) \approx \nabla_x \log p(x)$ を表現することをモデルが学習したことが観察できます :

def plot_gradients(model, data, plot_scatter=True):
    xx = np.stack(np.meshgrid(np.linspace(-1.5, 2.0, 50), np.linspace(-1.5, 2.0, 50)), axis=-1).reshape(-1, 2)
    scores = model(torch.from_numpy(xx).float()).detach()
    scores_norm = np.linalg.norm(scores, axis=-1, ord=2, keepdims=True)
    scores_log1p = scores / (scores_norm + 1e-9) * np.log1p(scores_norm)
    # Perform the plots
    plt.figure(figsize=(16,12))
    if (plot_scatter):
        plt.scatter(*data, alpha=0.3, color='red', edgecolor='white', s=40)
    plt.quiver(xx.T[0], xx.T[1], scores_log1p[:,0], scores_log1p[:,1], width=0.002, color='white')
    plt.xlim(-1.5, 2.0)
    plt.ylim(-1.5, 2.0)
plot_gradients(model, data)

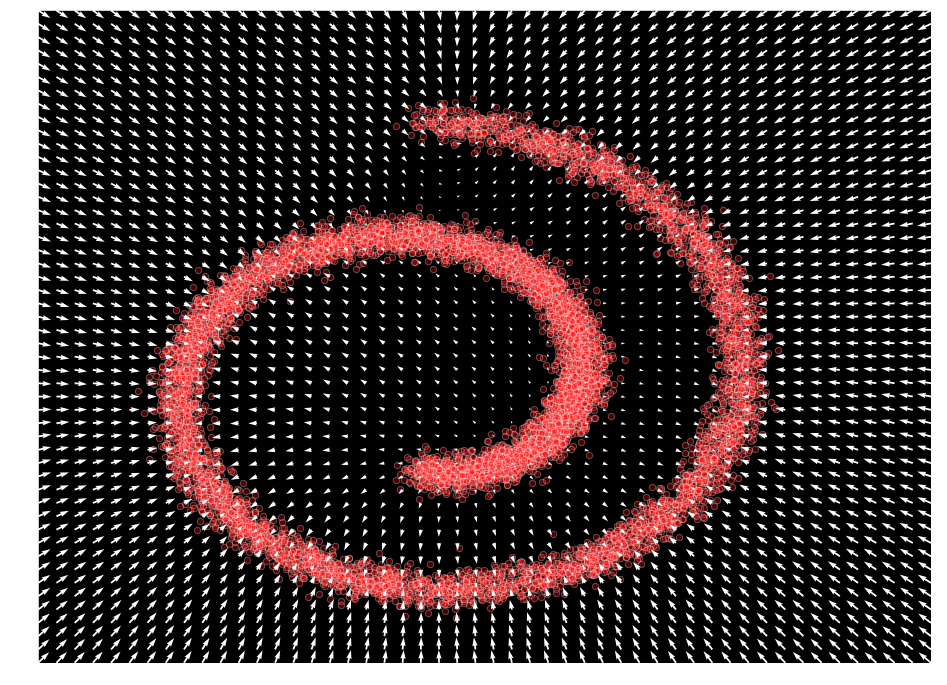
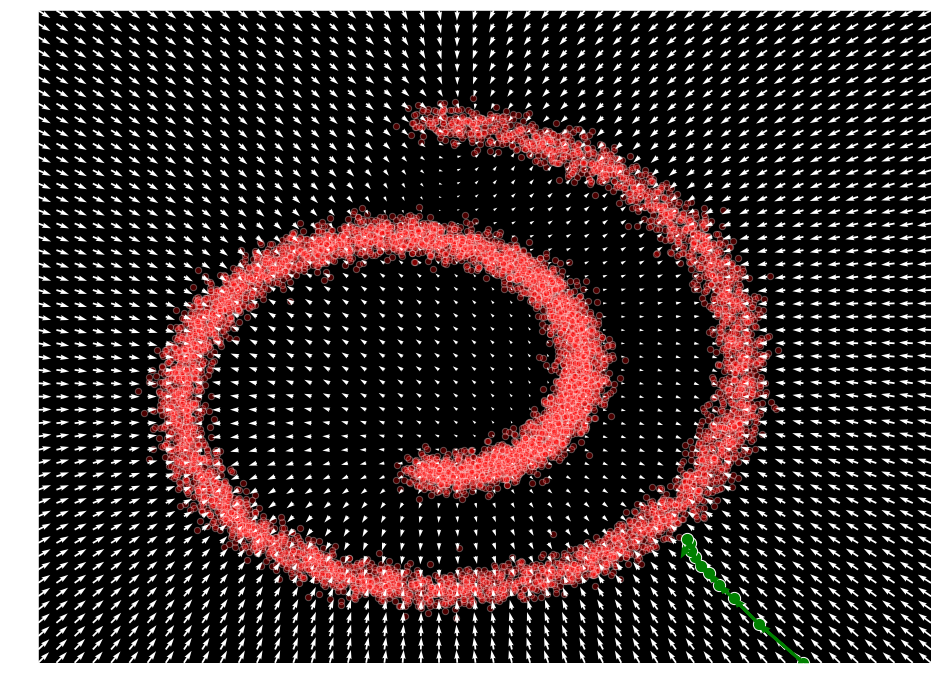
ランジュバン・サンプリング

ランジュバン動力学が、$\nabla_{\mathbf{x}} \log p(\mathbf{x})$ だけに依存して、密度 $p(\mathbf{x})$ から真のサンプルを生成可能な熱力学からのプロセスであることも見ました :

\[
\mathbf{x}_{t + 1} = \mathbf{x}_t + \frac{\epsilon}{2} \nabla_{\mathbf{x}_t} log p(\mathbf{x}_t) + \sqrt{\epsilon} \mathbf{z}_{t}
\]

ここで $\mathbf{z}_{t}\sim \mathcal{N}(\mathbf{0},\mathbf{I})$ そして $\epsilon \rightarrow 0, t \rightarrow \inf$ のもとで $\mathbf{x}_t$ は $p(\mathbf{x})$ からの正確なサンプルに収束します。これがスコアベースの生成モデリング・アプローチの裏のキーアイデアです :

def sample_langevin(model, x, n_steps=10, eps=1e-3, decay=.9, temperature=1.0):
    x_sequence = [x.unsqueeze(0)]
    for s in range(n_steps):
        z_t = torch.rand(x.size())
        x = x + (eps / 2) * model(x) + (np.sqrt(eps) * temperature * z_t)
        x_sequence.append(x.unsqueeze(0))
        eps *= decay
    return torch.cat(x_sequence)

x = torch.Tensor([1.5, -1.5])
samples = sample_langevin(model, x).detach()
plot_gradients(model, data)
plt.scatter(samples[:, 0], samples[:, 1], color='green', edgecolor='white', s=150)
# draw arrows for each mcmc step
deltas = (samples[1:] - samples[:-1])
deltas = deltas - deltas / torch.tensor(np.linalg.norm(deltas, keepdims=True, axis=-1)) * 0.04
for i, arrow in enumerate(deltas):
    plt.arrow(samples[i,0], samples[i,1], arrow[0], arrow[1], width=1e-4, head_width=2e-2, color="green", linewidth=3)

拡散モデル

拡散確率モデルは非平衡熱力学に基づき、元々は Sohl-Dickstein et al. [1] により提案されました。これらのモデルは 2 つの確率変数のマルコフ連鎖を表す 2 つの可逆過程に基づきます。一つの過程 $q(\mathbf{x}_{t}\mid\mathbf{x}_{t-1})$ は入力データに徐々にノイズを追加し (拡散または forward 過程と呼称)、信号を完全なノイズとなるまで破壊します。反対の方向では、逆過程 $p_{\theta}(\mathbf{x}_{t-1}\mid\mathbf{x}_{t})$ はこの拡散プロセスを逆にする方法 (ランダムノイズを高品質な波形 (= waveform) に変換) を学習しようとします。これは次の図で示されます、ここではモデル全体を見ることができます :

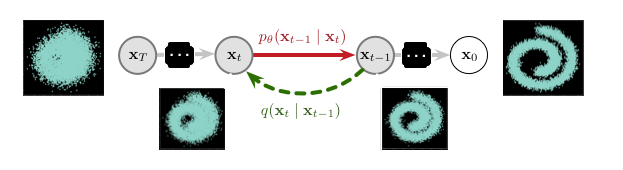
ご覧のように、forward (そして固定された) 過程 $q(\mathbf{x}_{t}\mid\mathbf{x}_{t-1})$ は各ステップで徐々にノイズを導入しています。反対に、逆 (パラメータ化された) 過程 $p_{\theta}(\mathbf{x}_{t-1}\mid\mathbf{x}_{t})$ は局所的な摂動をノイズ除去する方法を学習しなければなりません。従って、学習は巨大な数の小さい摂動を推定することを伴います、これは単一のポテンシャル関数で完全な分布を直接推定しようとするよりも扱いやすいです。

両者の過程はパラメータ化されたマルコフ連鎖として定義できますが、拡散過程は通常は各ステップで事前選択された量のノイズを注入するように単純化されます。逆の過程は変分推論を使用して訓練され、条件付きガウシアンとしてモデル化できます、これはニューラルネットワークのパラメータ化と扱いやすい推定を可能にします。

形式化

拡散モデルは潜在変数のシリーズ $\mathbf{x}_{1},\cdots,\mathbf{x}_{T}$ に基づきます、これらは ($\mathbf{x}_{0} \sim q(\mathbf{x}_{0})$ としてラベル付けされた) 与えられた入力データと同じ次元性を持ちます。そして、2 つの過程の動作を定義する必要があります :

\[
\text{forward (diffusion)} : q(\mathbf{x}_{t}\mid\mathbf{x}_{t-1}) \\
\text{reverse (parametric)} : p_{\theta}(\mathbf{x}_{t-1}\mid\mathbf{x}_{t})
\]

Forward 過程

forward 過程では、データ分布 $q(\mathbf{x}_{0})$ は、与えられた拡散レート $\beta$ で、マルコフ拡散カーネル $T_{\pi}(\mathbf{y}\mid\mathbf{y}’;\beta)$ の反復的な適用により解析的に扱いやすい分布 $\pi(\mathbf{y})$ に徐々に変換されます :

\[
q(\mathbf{x}_{t}\mid\mathbf{x}_{t-1}) = T_{\pi}(\mathbf{x}_{t}\mid\mathbf{x}_{t-1}; \beta_{t})
\]

この拡散カーネルは、次のように分散スケジュール $\beta_{1},\cdots,\beta_{T}$ が与えられたとき、ガウスノイズを徐々に注入するように設定できます :

\[
q(\mathbf{x}_{t}\mid\mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_{t} ; \sqrt{1-\beta_{t}}\mathbf{x}_{t-1},\beta_{t}\mathbf{I})
\]

完全な分布 $q(\mathbf{x}_{0:T})$ は拡散過程と呼ばれ次のように定義されます :

\[
q(\mathbf{x}_{0:T}) = q(\mathbf{x}_{0}) \prod_{t=1}^{T} q(\mathbf{x}_{t}\mid\mathbf{x}_{t-1})
\]

ここでは、定数分散スケジュールを持つ単純な forward 拡散過程の素朴な実装を実行する方法を示します :

def forward_process(x_start, n_steps, noise=None):
    """ Diffuse the data (t == 0 means diffused for 1 step) """
    x_seq = [x_start]
    for n in range(n_steps):
        x_seq.append((torch.sqrt(1 - betas[n]) * x_seq[-1]) + (betas[n] * torch.rand_like(x_start)))
    return x_seq
n_steps = 100
betas = torch.tensor([0.035] * n_steps)
dataset = torch.Tensor(data.T).float()
x_seq = forward_process(dataset, n_steps, betas)
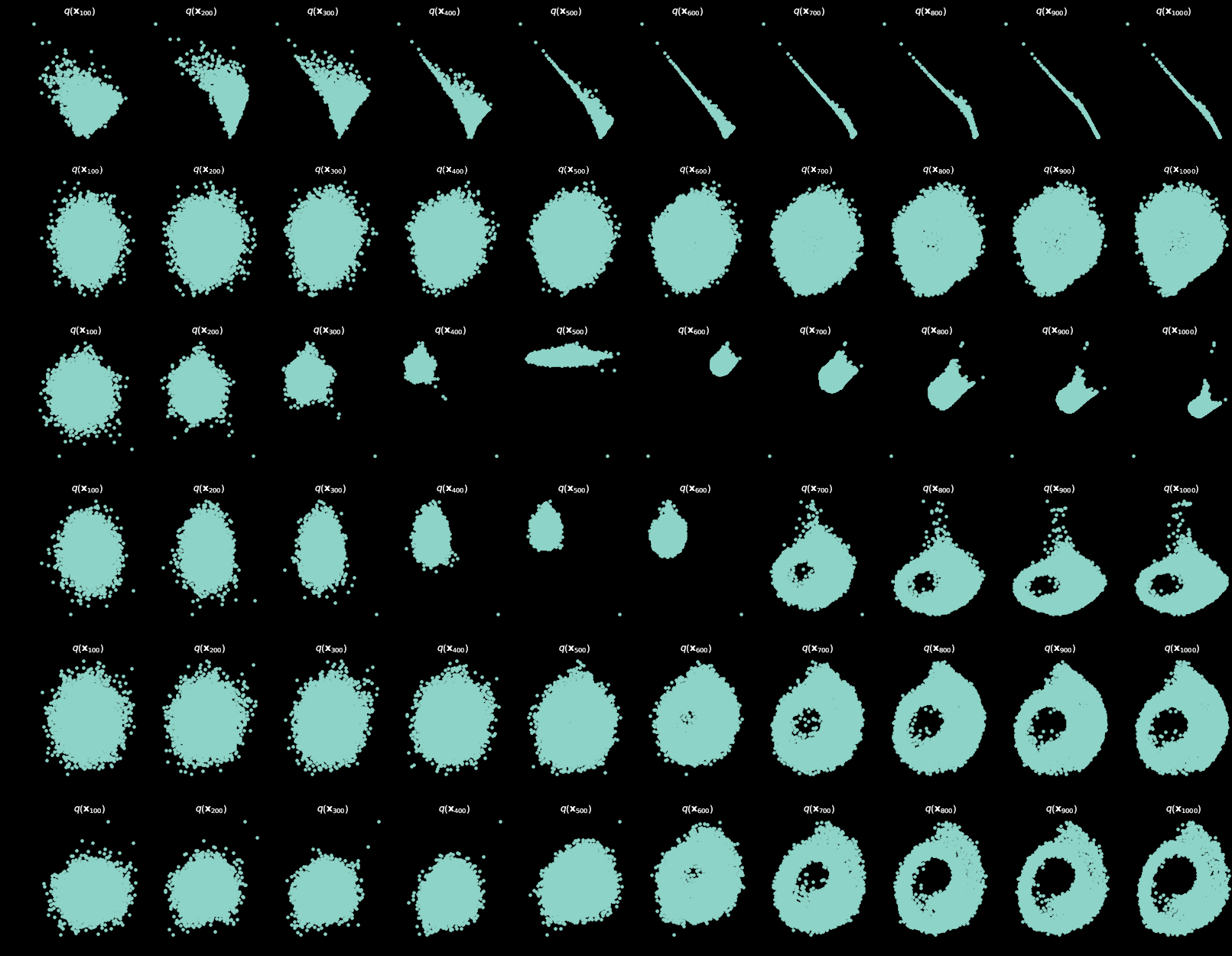
fig, axs = plt.subplots(1, 10, figsize=(28, 3))
for i in range(10):
    axs[i].scatter(x_seq[int((i / 10.0) * n_steps)][:, 0], x_seq[int((i / 10.0) * n_steps)][:, 1], s=10);
    axs[i].set_axis_off(); axs[i].set_title('$q(\mathbf{x}_{'+str(int((i / 10.0) * n_steps))+'})$')

以下の関数で提供されるように、$\beta_{1},\cdots,\beta_{n}$ に対して任意のタイプの分散スケジュールを定義することができます :

def make_beta_schedule(schedule='linear', n_timesteps=1000, start=1e-5, end=1e-2):
    if schedule == 'linear':
        betas = torch.linspace(start, end, n_timesteps)
    elif schedule == "quad":
        betas = torch.linspace(start ** 0.5, end ** 0.5, n_timesteps) ** 2
    elif schedule == "sigmoid":
        betas = torch.linspace(-6, 6, n_timesteps)
        betas = torch.sigmoid(betas) * (end - start) + start
    return betas

興味深いことに、forward 過程は任意の時間ステップ $t$ でサンプリング $\mathbf{x}_{t}$ を許容します。表記 $\alpha_{t}=1-\beta_{t}$ と $\bar{\alpha}_{t} = \prod_{s=1}^{t} \alpha_{s}$ を使用して、次を得ます :

\[
q(\mathbf{x}_{t}\mid\mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_{t} ; \sqrt{\bar{\alpha}_{t}}\mathbf{x}_{t-1},(1-\bar{\alpha}_{t})\mathbf{I})
\]

そして、このメカニズムを可能にするように拡散サンプリング関数を更新できます。これは、関数の前に計算する $\beta_{1},\cdots,\beta_{T}$ の与えられた分散スケジュールに依存することに注意してください。

betas = make_beta_schedule(schedule='sigmoid', n_timesteps=n_steps, start=1e-5, end=1e-2)
alphas = 1 - betas
alphas_prod = torch.cumprod(alphas, 0)
alphas_prod_p = torch.cat([torch.tensor([1]).float(), alphas_prod[:-1]], 0)
alphas_bar_sqrt = torch.sqrt(alphas_prod)
one_minus_alphas_bar_log = torch.log(1 - alphas_prod)
one_minus_alphas_bar_sqrt = torch.sqrt(1 - alphas_prod)

以下のコードで示されるように、これは forward 過程の非常に効率的な実装を実行することを可能にします、そこでは任意の与えられた時間ステップで直接サンプリングできます。

def extract(input, t, x):
    shape = x.shape
    out = torch.gather(input, 0, t.to(input.device))
    reshape = [t.shape[0]] + [1] * (len(shape) - 1)
    return out.reshape(*reshape)
def q_sample(x_0, t, noise=None):
    if noise is None:
        noise = torch.randn_like(x_0)
    alphas_t = extract(alphas_bar_sqrt, t, x_0)
    alphas_1_m_t = extract(one_minus_alphas_bar_sqrt, t, x_0)
    return (alphas_t * x_0 + alphas_1_m_t * noise)
fig, axs = plt.subplots(1, 10, figsize=(28, 3))
for i in range(10):
    q_i = q_sample(dataset, torch.tensor([i * 10]))
    axs[i].scatter(q_i[:, 0], q_i[:, 1], s=10);
    axs[i].set_axis_off(); axs[i].set_title('$q(\mathbf{x}_{'+str(i*10)+'})$')

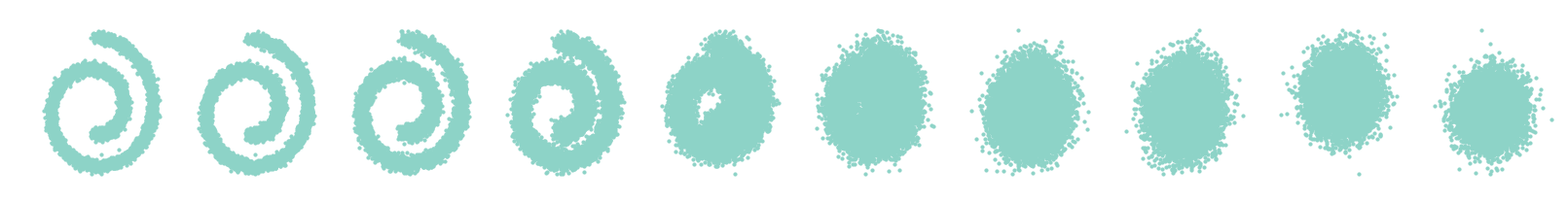
訓練のためには、この過程の事後分布の平均と分散へのアクセスも持つ必要があることに注意してください。

posterior_mean_coef_1 = (betas * torch.sqrt(alphas_prod_p) / (1 - alphas_prod))
posterior_mean_coef_2 = ((1 - alphas_prod_p) * torch.sqrt(alphas) / (1 - alphas_prod))
posterior_variance = betas * (1 - alphas_prod_p) / (1 - alphas_prod)
posterior_log_variance_clipped = torch.log(torch.cat((posterior_variance[1].view(1, 1), posterior_variance[1:].view(-1, 1)), 0)).view(-1)

def q_posterior_mean_variance(x_0, x_t, t):
    coef_1 = extract(posterior_mean_coef_1, t, x_0)
    coef_2 = extract(posterior_mean_coef_2, t, x_0)
    mean = coef_1 * x_0 + coef_2 * x_t
    var = extract(posterior_log_variance_clipped, t, x_0)
    return mean, var

逆過程

学習させることを目的とする生成分布は逆の軌跡を遂行するために訓練され、ガウスノイズから始めて徐々に局所摂動を除去します。そのため逆過程は与えられた扱いやすい分布 $p(\mathbf{x}_{T})=\pi(\mathbf{x}_{T})$ から始めて次のように記述されます :

\[
p_{\theta}(\mathbf{x}_{0:T}) = p(\mathbf{x}_{T}) \prod_{t=1}^{T} p_{\theta}(\mathbf{x}_{t-1}\mid\mathbf{x}_{t})
\]

この過程の遷移の各々は条件付きガウシアンとして単純に定義できます (note: これは VAE の定義を連想させます)。従って、学習の間、ガウシアン拡散カーネルに対する平均と共分散だけが訓練される必要があります :
\[
p_{\theta}(\mathbf{x}_{t-1}\mid\mathbf{x}_{t}) = \mathcal{N}(\mathbf{x}_{t-1} ; \mathbf{\mu}_{\theta}(\mathbf{x}_{t},t),\mathbf{\Sigma}_{\theta}(\mathbf{x}_{t},t))
\]

平均 $\mathbf{\mu}_{\theta}(\mathbf{x}_{t},t)$ と共分散 $\mathbf{\Sigma}_{\theta}(\mathbf{x}_{t},t)$ を定義する 2 つの関数は深層ニューラルネットワークによりパラメータ化できます。これらの関数は $t$ によりパラメータ化されることにも注意してください、これは総ての時間ステップに対して単一のモデルが利用できることを意味しています。

ここでは、この過程の素朴な実装を示します、ここでは分散を推論する与えられたモデルを持ちます。このモデルは総ての時間ステップに渡り共有されますが、その前記の時間ステップで条件付けられることに注意してください。

import torch.nn.functional as F
class ConditionalLinear(nn.Module):
    def __init__(self, num_in, num_out, n_steps):
        super(ConditionalLinear, self).__init__()
        self.num_out = num_out
        self.lin = nn.Linear(num_in, num_out)
        self.embed = nn.Embedding(n_steps, num_out)
        self.embed.weight.data.uniform_()

    def forward(self, x, y):
        out = self.lin(x)
        gamma = self.embed(y)
        out = gamma.view(-1, self.num_out) * out
        return out
class ConditionalModel(nn.Module):
    def __init__(self, n_steps):
        super(ConditionalModel, self).__init__()
        self.lin1 = ConditionalLinear(2, 128, n_steps)
        self.lin2 = ConditionalLinear(128, 128, n_steps)
        self.lin3 = nn.Linear(128, 4)
    
    def forward(self, x, y):
        x = F.softplus(self.lin1(x, y))
        x = F.softplus(self.lin2(x, y))
        return self.lin3(x)
model = ConditionalModel(n_steps)
    
def p_mean_variance(model, x, t):
    # Go through model
    out = model(x, t)
    # Extract the mean and variance
    mean, log_var = torch.split(out, 2, dim=-1)
    var = torch.exp(log_var)
    return mean, log_var

ご覧のように、この逆過程は与えられた時間ステップに対して平均と log 分散の値を推論することから構成されます。そして、対応するモデルを学習したならば、任意の与えられた時間ステップのノイズ除去を実行することができます、与えられた時間ステップにおけるサンプル $\mathbf{x}_{t}$ とその時間ステップ $t$ の両者を提供することによります、これは $\mathbf{\mu}_{\theta}(\mathbf{x}_{t},t)$ と $\mathbf{\Sigma}_{\theta}(\mathbf{x}_{t},t)$ に対するモデルを条件付けるために使用できます。

def p_sample(model, x, t):
    mean, log_var = p_mean_variance(model, x, torch.tensor(t))
    noise = torch.randn_like(x)
    shape = [x.shape[0]] + [1] * (x.ndimension() - 1)
    nonzero_mask = (1 - (t == 0))
    sample = mean + torch.exp(0.5 * log_var) * noise
    return (sample)

最後に、モデルからのサンプル取得は逆のマルコフ連鎖全体を実行することにより与えられえます、ターゲット分布からサンプルを取得するために正規分布から始めます。この過程は多くのステップを持つ場合非常に遅い可能性があることに注意してください、与えられた $\mathbf{x}_{t}$ が続く $\mathbf{x}_{t-1}$ を推論するのを待つ必要があるからです。

def p_sample_loop(model, shape):
    cur_x = torch.randn(shape)
    x_seq = [cur_x]
    for i in reversed(range(n_steps)):
        cur_x = p_sample(model, cur_x, i)
        x_seq.append(cur_x)
    return x_seq

モデル確率

生成モデルの完全な確率は次のように定義されます :

\[
p_{\theta}(\mathbf{x}_{0}) = \int p_{\theta}(\mathbf{x}_{0:T})d\mathbf{x}_{1:T}
\]

一見すると、この積分は扱いにくいように見えます。しかし、変分推論と同様のアプローチを使用すればこの積分は以下のように書き換えることができます :

\[
\begin{align}
p_{\theta}(\mathbf{x}_{0}) &= \int p_{\theta}(\mathbf{x}_{0:T})\frac{q(\mathbf{x}_{1:T}\mid\mathbf{x}_{0})}{q(\mathbf{x}_{1:T}\mid\mathbf{x}_{0})} d\mathbf{x}_{1:T} \\
&= \int q(\mathbf{x}_{1:T}\mid\mathbf{x}_{0}) \frac{p(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}\mid\mathbf{x}_{0})} d\mathbf{x}_{1:T}
\end{align}
\]

訓練

前の式でイェンセンの不等式を使用することで、訓練は負の対数尤度の変分境界 (= bound) を最適化することにより遂行できる可能性があることが分かります :

\[
\begin{align}
\mathbb{E}\left[-\log p_{\theta}(\mathbf{x}_{0}) \right] & \leq \mathbb{E}_{q}\left[-\log \frac{p_{\theta}(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \mid \mathbf{x}_{0})} \right] \\
\mathcal{L} & = \mathbb{E}_{q}\left[ -\log p(\mathbf{x}_{T}) – \sum_{t\geq 1} \log \frac{p_{\theta}(\mathbf{x}_{t-1}\mid\mathbf{x}_{t})}{q(\mathbf{x}_{t}\mid\mathbf{x}_{t-1})} \right]
\end{align}
\]

従って、効率的な訓練は勾配降下により $\mathcal{L}$ のランダム項を最適化することで可能になります。

この損失を最適化するには、幾つかの計算ツールが必要です、特に 2 つのガウシアン間の KL ダイバージェンス、そしてガウシアンのエントロピーです。

def normal_kl(mean1, logvar1, mean2, logvar2):
    kl = 0.5 * (-1.0 + logvar2 - logvar1 + torch.exp(logvar1 - logvar2) + ((mean1 - mean2) ** 2) * torch.exp(-logvar2))
    return kl

def entropy(val):
    return (0.5 * (1 + np.log(2. * np.pi))) + 0.5 * np.log(val)

訓練損失

Sohl-Dickstein et al. [1] によるオリジナルの論文では、この損失は以下に帰着できることが示されています :

\[
\begin{align}
K = -\mathbb{E}_{q}[ &D_{KL}(q(\mathbf{x}_{t-1}\mid\mathbf{x}_{t},\mathbf{x}_{0}) \Vert p_{\theta}(\mathbf{x}_{t-1}\mid\mathbf{x}_{t})) \\
&+ H_{q}(\mathbf{X}_{T}\vert\mathbf{X}_{0}) – H_{q}(\mathbf{X}_{1}\vert\mathbf{X}_{0}) – H_{p}(\mathbf{X}_{T})]
\end{align}
\]

こうして、この損失の総てのパーツが非常に簡単に推定できます、総てのケースでガウス分布を扱っているからです。

def compute_loss(true_mean, true_var, model_mean, model_var):
    # the KL divergence between model transition and posterior from data
    KL = normal_kl(true_mean, true_var, model_mean, model_var).float()
    # conditional entropies H_q(x^T|x^0) and H_q(x^1|x^0)
    H_start = entropy(betas[0].float()).float()
    beta_full_trajectory = 1. - torch.exp(torch.sum(torch.log(alphas))).float()
    H_end = entropy(beta_full_trajectory.float()).float()
    H_prior = entropy(torch.tensor([1.])).float()
    negL_bound = KL * n_steps + H_start - H_end + H_prior
    # the negL_bound if this was an isotropic Gaussian model of the data
    negL_gauss = entropy(torch.tensor([1.])).float()
    negL_diff = negL_bound - negL_gauss
    L_diff_bits = negL_diff / np.log(2.)
    L_diff_bits_avg = L_diff_bits.mean()
    return L_diff_bits_avg

ランダムな時間ステップの訓練

モデルが訓練される方法は少し直感的には理解しにくいものです、何故ならばバッチ入力の各々に対してランダムに時間ステップを選択して訓練するからです。DDIM レポジトリから引用された実装は antithetic サンプリングの形式を提供し、これは異なる連鎖の対称的なポイントが一緒に訓練されることを保証することを可能にします。従って、最終的な手順は、まず与えられた (ランダムな) 時間ステップで各入力の forward 過程を実行すること (拡散の実行) から構成されます。そしてこのサンプルで反対の過程を実行し、損失を計算します。

def loss_likelihood_bound(model, x_0):
    batch_size = x_0.shape[0]
    # Select a random step for each example
    t = torch.randint(0, n_steps, size=(batch_size // 2 + 1,))
    t = torch.cat([t, n_steps - t - 1], dim=0)[:batch_size].long()
    # Perform diffusion for step t
    x_t = q_sample(x_0, t)
    # Compute the true mean and variance
    true_mean, true_var = q_posterior_mean_variance(x_0, x_t, t)
    # Infer the mean and variance with our model
    model_mean, model_var = p_mean_variance(model, x_t, t)
    # Compute the loss
    return compute_loss(true_mean, true_var, model_mean, model_var)

この損失を以下の訓練ロープで非常に簡単に最適化できます :

model = ConditionalModel(n_steps)
optimizer = optim.Adam(model.parameters(), lr=1e-3)
dataset = torch.tensor(data.T).float()
batch_size = 128
for t in range(5001):
    # X is a torch Variable
    permutation = torch.randperm(dataset.size()[0])
    for i in range(0, dataset.size()[0], batch_size):
        # Retrieve current batch
        indices = permutation[i:i+batch_size]
        batch_x = dataset[indices]
        # Compute the loss.
        loss = loss_likelihood_bound(model, batch_x)
        # Before the backward pass, zero all of the network gradients
        optimizer.zero_grad()
        # Backward pass: compute gradient of the loss with respect to parameters
        loss.backward()
        # Perform gradient clipping
        torch.nn.utils.clip_grad_norm_(model.parameters(), 1.)
        # Calling the step function to update the parameters
        optimizer.step()
    # Print loss
    if (t % 1000 == 0):
        print(loss)
        x_seq = p_sample_loop(model, dataset.shape)
        fig, axs = plt.subplots(1, 10, figsize=(28, 3))
        for i in range(1, 11):
            cur_x = x_seq[i * 10].detach()
            axs[i-1].scatter(cur_x[:, 0], cur_x[:, 1], s=10);
            axs[i-1].set_axis_off(); axs[i-1].set_title('$q(\mathbf{x}_{'+str(i*100)+'})$')

tensor(134.9538, grad_fn=<MeanBackward0>)
tensor(-2.4417, grad_fn=<MeanBackward0>)
tensor(3.9380, grad_fn=<MeanBackward0>)
tensor(2.4344, grad_fn=<MeanBackward0>)
tensor(1.6676, grad_fn=<MeanBackward0>)
tensor(1.8195, grad_fn=<MeanBackward0>)

ノイズ除去拡散確率モデル (DDPM)

非常に最近の論文で、Ho et al. [1] は結果の品質を強化することを可能にする幾つかの拡張を提案することにより拡散モデルのアイデアを構築しました。最初に、mean 関数に対して次のパラメータ化に依拠することを提案しました :

\[
\mathbf{\mu}_{\theta}(\mathbf{x}_{t}, t) = \frac{1}{\sqrt{\alpha_{t}}} \left( (\mathbf{x}_{t} – \frac{\beta_{t}}{\sqrt{1 – \bar{\alpha}}_{t}} \mathbf{\epsilon}_{\theta} (\mathbf{x}_{t}, t) \right)
\]

今、モデルはノイズ関数の形式を直接的に出力するように訓練されることに注意してください、これはサンプリング・プロセスで使用されます。更に、著者らはどちらかと言えば固定された分散関数を使用することを提案しています :

\[
\mathbf{x}_{t-1} = \frac{1}{\sqrt{\alpha_{t}}} \left( \mathbf{x}_{t} – \frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha_{t}}}} \mathbf{\epsilon}_{\theta}(\mathbf{x}_{t}, t) \right) + \sigma_{t}\mathbf{z}
\]

これは次のように逆過程に対する新しいサンプリング手順に繋がります (正しい次元性を出力するようにモデルを素早く再定義もします)。

class ConditionalModel(nn.Module):
    def __init__(self, n_steps):
        super(ConditionalModel, self).__init__()
        self.lin1 = ConditionalLinear(2, 128, n_steps)
        self.lin2 = ConditionalLinear(128, 128, n_steps)
        self.lin3 = ConditionalLinear(128, 128, n_steps)
        self.lin4 = nn.Linear(128, 2)
    
    def forward(self, x, y):
        x = F.softplus(self.lin1(x, y))
        x = F.softplus(self.lin2(x, y))
        x = F.softplus(self.lin3(x, y))
        return self.lin4(x)

def p_sample(model, x, t):
    t = torch.tensor([t])
    # Factor to the model output
    eps_factor = ((1 - extract(alphas, t, x)) / extract(one_minus_alphas_bar_sqrt, t, x))
    # Model output
    eps_theta = model(x, t)
    # Final values
    mean = (1 / extract(alphas, t, x).sqrt()) * (x - (eps_factor * eps_theta))
    # Generate z
    z = torch.randn_like(x)
    # Fixed sigma
    sigma_t = extract(betas, t, x).sqrt()
    sample = mean + sigma_t * z
    return (sample)

特に、forward 過程の事後分布は $\mathbf{x}_{0}$ で条件付けられるとき扱いやすいです :

\[
\begin{align}
q(\mathbf{x}_{t}\mid\mathbf{x}_{t-1}) &= \mathcal{N}(\mathbf{x}_{t-1} ; \mathbf {1-\beta_{t}}\mathbf{x}_{t-1},\beta_{t}\mathbf{I})
\end{align}
\]

そして次のように対応する平均 $\tilde{\mathbf{\mu}}_{t}(\mathbf{x}_{t},\mathbf{x}_{0})$ と分散 $\tilde{\beta}$ を取得できます :

\[
\begin{align}
\tilde{\mathbf{\mu}}_{t}(\mathbf{x}_{t},\mathbf{x}_{0}) &= \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_{t}}{1 – \bar{\alpha}_{t}}\mathbf{x}_{0} + \frac{\sqrt{\bar{\alpha}_{t}}(1 – \bar{\alpha}_{t-1})}{1 – \bar{\alpha}_{t}}\mathbf{x}_{t}\\
\tilde{\beta}_{t} &= \frac{1 – \bar{\alpha}_{t-1}}{1 – \bar{\alpha}_{t}}\beta_{t}
\end{align}
\]

DDPM で訓練

$\mathcal{L}$ を KL ダイバージェンスの合計として書き換えることにより更なる改良が分散のリダクションによりもたらされます :

\[
\begin{align}
\mathcal{L} &= \mathbb{E}_{q}\left[ \mathcal{L}_{T} + \sum_{t>1} \mathcal{L}_{t-1} + \mathcal{L}_{0} \right] \\
\mathcal{L}_{T} &= D_{KL}(q(\mathbf{x}_{T}\mid\mathbf{x}_{0}) \Vert p(\mathbf{x}_{T})) \\
\mathcal{L}_{t-1} &= D_{KL}(q(\mathbf{x}_{t-1}\mid\mathbf{x}_{t},\mathbf{x}_{0}) \Vert p_{\theta}(\mathbf{x}_{t-1}\mid\mathbf{x}_{t})) \\
\mathcal{L}_{0} &= – \log p_{\theta}(\mathbf{x}_{0}\mid\mathbf{x}_{1})
\end{align}
\]

この等式で定義される総ての KL ダイバージェンスはガウシアンと比較していて、これはそれらが閉形式解を持つことを意味しています。

def approx_standard_normal_cdf(x):
    return 0.5 * (1.0 + torch.tanh(torch.tensor(np.sqrt(2.0 / np.pi)) * (x + 0.044715 * torch.pow(x, 3))))

def discretized_gaussian_log_likelihood(x, means, log_scales):
    # Assumes data is integers [0, 255] rescaled to [-1, 1]
    centered_x = x - means
    inv_stdv = torch.exp(-log_scales)
    plus_in = inv_stdv * (centered_x + 1. / 255.)
    cdf_plus = approx_standard_normal_cdf(plus_in)
    min_in = inv_stdv * (centered_x - 1. / 255.)
    cdf_min = approx_standard_normal_cdf(min_in)
    log_cdf_plus = torch.log(torch.clamp(cdf_plus, min=1e-12))
    log_one_minus_cdf_min = torch.log(torch.clamp(1 - cdf_min, min=1e-12))
    cdf_delta = cdf_plus - cdf_min
    log_probs = torch.where(x < -0.999, log_cdf_plus, torch.where(x > 0.999, log_one_minus_cdf_min, torch.log(torch.clamp(cdf_delta, min=1e-12))))
    return log_probs

これは以下で実装されているように新しい損失関数に繋がります (この目的関数は最適化自身には大きな変更は与えないことに注意してください) :

def loss_variational(model, x_0):
    batch_size = x_0.shape[0]
    # Select a random step for each example
    t = torch.randint(0, n_steps, size=(batch_size // 2 + 1,))
    t = torch.cat([t, n_steps - t - 1], dim=0)[:batch_size].long()
    # Perform diffusion for step t
    x_t = q_sample(x_0, t)
    # Compute the true mean and variance
    true_mean, true_var = q_posterior_mean_variance(x_0, x_t, t)
    # Infer the mean and variance with our model
    model_mean, model_var = p_mean_variance(model, x_t, t)
    # Compute the KL loss
    kl = normal_kl(true_mean, true_var, model_mean, model_var)
    kl = torch.mean(kl.view(batch_size, -1), dim=1) / np.log(2.)
    # NLL of the decoder
    decoder_nll = -discretized_gaussian_log_likelihood(x_0, means=model_mean, log_scales=0.5 * model_var)
    decoder_nll = torch.mean(decoder_nll.view(batch_size, -1), dim=1) / np.log(2.)
    # At the first timestep return the decoder NLL, otherwise return KL(q(x_{t-1}|x_t,x_0) || p(x_{t-1}|x_t))
    output = torch.where(t == 0, decoder_nll, kl)
    return output.mean(-1)

ノイズ除去スコアマッチングへの損失の簡略化

Ho et al. [1] による論文は逆過程の平均に対する新しいパラメータ化を提案しています :

\[
\mathbf{x}_{t-1} = \frac{1}{\sqrt{\alpha_{t}}} \left( \mathbf{x}_{t} – \frac{1 – \alpha_{t}}{\sqrt{1-\bar{\alpha_{t}}}} \mathbf{\epsilon}_{\theta}(\mathbf{x}_{t}, t) \right) + \sigma_{t}\mathbf{z}
\]

このパラメータ化に基づき、訓練目的関数は次のように単純化できることを彼らは示しています :

\[
\mathcal{L}_{t-1}-C=\mathbb{E}_{\mathbf{x}_{0},\mathbf{\epsilon}}\left[ \frac{\beta_{t}^{2}}{2\sigma_{t}^{2}\alpha_{t}(1-\bar{\alpha}_{t})} \Vert \epsilon – \epsilon_{\theta}(\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0} + \sqrt{1 – \bar{\alpha}_{t}}\mathbf{\epsilon}, t) \Vert^{2} \right]
\]

これは $t$ によりインデックスされた複数のノイズスケールに渡るノイズ除去スコアマッチングに似ています。

更に単純化された訓練 objective

著者らは損失の最初における複雑な要因を完全に取り除くことがサンプル品質に有益であるという事実を考察しています。これは objective を次のひょうに更に単純化します :

\[
\mathcal{L}_{\text{simple}}=\mathbb{E}_{t, \mathbf{x}_{0},\mathbf{\epsilon}}\left[ \Vert \epsilon – \epsilon_{\theta}(\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0} + \sqrt{1 – \bar{\alpha}_{t}}\mathbf{\epsilon}, t) \Vert^{2} \right].
\]

この objective は今ではノイズ除去スコアマッチング定式化に非情に近く似ていることが分かります。更に、それは極めて単純な実装を提供します。

def noise_estimation_loss(model, x_0):
    batch_size = x_0.shape[0]
    # Select a random step for each example
    t = torch.randint(0, n_steps, size=(batch_size // 2 + 1,))
    t = torch.cat([t, n_steps - t - 1], dim=0)[:batch_size].long()
    # x0 multiplier
    a = extract(alphas_bar_sqrt, t, x_0)
    # eps multiplier
    am1 = extract(one_minus_alphas_bar_sqrt, t, x_0)
    e = torch.randn_like(x_0)
    # model input
    x = x_0 * a + e * am1
    output = model(x, t)
    return (e - output).square().mean()

指数移動平均 (EMA) による訓練の安定化

このアイデアは殆どの実装で見られ、モデルモメンタムの形式の実装を可能にします。モデルの重みを直接更新する代わりに、重みの前の値のコピーを保持してから、重みの前のバージョンと新しいバージョン間の加重平均を更新します。ここで、DDIM レポジトリで提案された実装を最利用しています。

class EMA(object):
    def __init__(self, mu=0.999):
        self.mu = mu
        self.shadow = {}

    def register(self, module):
        for name, param in module.named_parameters():
            if param.requires_grad:
                self.shadow[name] = param.data.clone()

    def update(self, module):
        for name, param in module.named_parameters():
            if param.requires_grad:
                self.shadow[name].data = (1. - self.mu) * param.data + self.mu * self.shadow[name].data

    def ema(self, module):
        for name, param in module.named_parameters():
            if param.requires_grad:
                param.data.copy_(self.shadow[name].data)

    def ema_copy(self, module):
        module_copy = type(module)(module.config).to(module.config.device)
        module_copy.load_state_dict(module.state_dict())
        self.ema(module_copy)
        return module_copy

    def state_dict(self):
        return self.shadow

    def load_state_dict(self, state_dict):
        self.shadow = state_dict

訓練ループは最終的に以下のコードで得られます :

model = ConditionalModel(n_steps)
optimizer = optim.Adam(model.parameters(), lr=1e-3)
dataset = torch.tensor(data.T).float()
# Create EMA model
ema = EMA(0.9)
ema.register(model)
# Batch size
batch_size = 128
for t in range(1000):
    # X is a torch Variable
    permutation = torch.randperm(dataset.size()[0])
    for i in range(0, dataset.size()[0], batch_size):
        # Retrieve current batch
        indices = permutation[i:i+batch_size]
        batch_x = dataset[indices]
        # Compute the loss.
        loss = noise_estimation_loss(model, batch_x)
        # Before the backward pass, zero all of the network gradients
        optimizer.zero_grad()
        # Backward pass: compute gradient of the loss with respect to parameters
        loss.backward()
        # Perform gradient clipping
        torch.nn.utils.clip_grad_norm_(model.parameters(), 1.)
        # Calling the step function to update the parameters
        optimizer.step()
        # Update the exponential moving average
        ema.update(model)
    # Print loss
    if (t % 100 == 0):
        print(loss)
        x_seq = p_sample_loop(model, dataset.shape)
        fig, axs = plt.subplots(1, 10, figsize=(28, 3))
        for i in range(1, 11):
            cur_x = x_seq[i * 10].detach()
            axs[i-1].scatter(cur_x[:, 0], cur_x[:, 1], s=10);
            #axs[i-1].set_axis_off(); 
            axs[i-1].set_title('$q(\mathbf{x}_{'+str(i*100)+'})$')

tensor(1.1240, grad_fn=<MeanBackward0>)
tensor(0.5651, grad_fn=<MeanBackward0>)
tensor(0.4491, grad_fn=<MeanBackward0>)
tensor(0.8212, grad_fn=<MeanBackward0>)
tensor(0.9979, grad_fn=<MeanBackward0>)
tensor(0.4364, grad_fn=<MeanBackward0>)
tensor(0.6083, grad_fn=<MeanBackward0>)
tensor(0.6552, grad_fn=<MeanBackward0>)
tensor(0.7025, grad_fn=<MeanBackward0>)
tensor(1.1096, grad_fn=<MeanBackward0>)

参考文献

以上

2022年9月
月	火	水	木	金	土	日
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30